Dessins et manipulations d'images en Python

Que fait le programme suivant ? Vous pouvez le récupérer dans le fichier start.py pour le tester (en l'ouvrant avec IDLE, et en l'évaluant avec F5).

def sep():
  print("------------")

print ("Hello !")

sep()
a = 5

print ("a, a*a")
print (a,  a*a)
print ("a vaut", a, "et a*a vaut",  a*a)

sep()
if a*a == a**a:
  print("OK")

sep()
if a*a == a**a:
  print("OK")
else:
  print("KO")

sep()
def f():
  print (2)

a = f()
print ("a = ", a)

sep()
def g():
  return 2

b = g()
print ("b = ", b)

sep()
for n in range(5):
  print (n)

sep()
for n in range(10, 100, 5):
  print (n)

Dans cette partie, nous allons reprogrammer la suite de Syracuse, en partant d'un entier n. Cette suite d'entiers est facile à définir:

• le premier nombre de la suite est n.
• si n est égal à 1, la suite s'arrête.
• si n est différent de 1, on construit le terme suivant de la façon suivante: si n est pair, le terme suivant est n/2. Sinon, le terme suivant est 3n+1.

Par exemple, si on part de l'entier 9 comme valeur de n, la suite d'entiers obtenue est

9, 28, 14, 7, 22, 11, 34, 17, 52, 26, 13, 40, 20, 10, 5, 16, 8, 4, 2, 1

Les mathématiciens pensent que la suite finit toujours par arriver à l'entier 1, comme dans l'exemple précédent. Mais personne n'est jamais arrivé à le prouver. Dans cette partie, on va essayer de vérifier que la suite arrive toujours à 1 si on part d'un entier entre 1 et 1000000.

Pour ces questions, un fichier squelette syracuse.py est fourni.

1. Commencer par écrire une fonction syracuse(n) qui prend en argument un entier n, et retourne la valeur n/2 si n est pair, ou 3n+1 sinon.
   Rappels:
   • La division de nombres entiers se note // et la multiplication se note *.
   • Pour faire retourner la valeur calculée par une fonction, on utilise le mot-clé return.
2. En se servant de cette fonction, écrire une nouvelle fonction suite_syracuse(n) qui prend en argument un entier n, et affiche la suite obtenue à partir de n (en espérant que cette suite est finie, c'est-à-dire qu'elle arrive à un moment à la valeur 1).
   Note: cette fonction ne retournera rien: elle se contente de produire un affichage, grâce à l'utilisation de la fonction print(...).
3. Écrire une fonction longueur_syracuse(n) qui n'affiche rien, mais qui retourne la longueur de la suite obtenue en partant de la valeur n. Par exemple, partant de la valeur 9, la fonction devra afficher 20 (qui est la longueur de la suite ci-dessus).

   Pour cela, on utilise une variable longueur initialisée à 1, et que l'on augmente d'une unité à chaque fois qu'un nouveau nombre de la suite est calculé.

4. Écrire une fonction longueur_syracuse_jusqua(n) qui prend en argument un entier n, et qui affiche, pour chaque entier k entre 1 et n, la valeur de k et la longueur de la suite lorsqu'on part de l'entier k.
5. Écrire une fonction indice_et_longueur_maximale(n) qui prend en argument un entier n, et qui retourne 2 valeurs:
   • le premier entier entre 1 et n pour lequel la longueur de la suite de

   Syracuse est la plus grande, et

   • la longueur de cette suite.

   En langage Python, on peut faire retourner 2 valeurs à la fois, par exemple return 1, 2 retourne la valeur 1 et la valeur 2.

6. Utiliser la fonction indice_et_longueur_maximale(n) pour calculer le premier entier entre 0 et 1000000 qui donne la plus longue suite de Syracuse.

Dans cette partie, on va utiliser le module turtle pour faire des dessins. Dans un nouveau fichier, commencer par écrire la ligne suivante:

from turtle import *

Les fonctions du module turtle sont maintenant disponibles. Les lignes suivantes permettent d'afficher la fenêtre de dessin, et d'initialiser le mode de couleurs.

Screen()

colormode(255)

On peut ensuite déplacer une "tortue", qui laisse une trace de crayon lors de ses déplacements. Les fonctions les plus utiles pour dessiner avec cette tortue sont les suivantes:

reset()	Efface l'écran
goto(x,y)	Va au point de coordonnées (x, y)
forward(d)	Avance de la distance d
up()	Lève le crayon : si on fait un goto() ensuite, la tortue ne laisse pas de trace
down()	Abaisse le crayon : si on fait un goto() ensuite, la tortue laisse une trace
color(r,v,b)	Change la couleur du crayon. r (rouge), v (vert) et b (bleu) sont entre 0 et 255
setheading(angle)	Modifie la direction de la tortue
left(angle)	Tourne à gauche
right(angle)	Tourne à droite
width(e)	Change l'épaisseur du crayon à e.
speed(vitesse)	Ajuste la vitesse de la tortue, par exemple 'fastest' ou 'normal'

Comme on va tracer des polygones, on peut utiliser l'instruction for qui permet de répéter le même bloc d'instructions pour plusieurs valeurs d'une variable.

Un squelette de programme est fourni dans le fichier tortue.py, mais les fonctions demandées sont vides : il ne reste plus qu'à les écrire…

1. Écrire une fonction carre(taille) qui dessine un carré dont les bords ont la taille donnée en paramètre.
2. Écrire une fonction polygone(taille, cotes) qui dessine un polygone régulier dont la taille et le nombre de côtés sont donnés en paramètres.
3. Tester la fonction polygone en écrivant une fonction triangle(taille), puis en dessinant un… cercle grâce à la fonction polygone.
4. Écrire une fonction rosace(taille, cote) qui dessine une rosace en dessinant plusieurs polygones dont la taille et le côté sont donnés en paramètres. Le premier côté du k-ième polygone dessiné sera incliné d'un angle 10k, et on fera varier cet angle de 0 à 350 degrés, par pas de 10 degrés. On dessine donc au total 36 polygones, inclinés de 10 degrés en 10 degrés.
5. Écrire une fonction rosace_coloree(taille, cote) qui fait la même chose que la fonction précédente, mais qui en plus change progressivement la couleur des polygones dessinés. On part d'une première couleur, par exemple rouge (noté 255,0,0 dans le codage r,v,b) pour arriver à une couleur de fin, par exemple bleu (noté 0,0,255). A chaque nouveau polygone, on modifie progressivement et uniformément la couleur. Par exemple, rosace_coloree(100,5) donne ce dessin: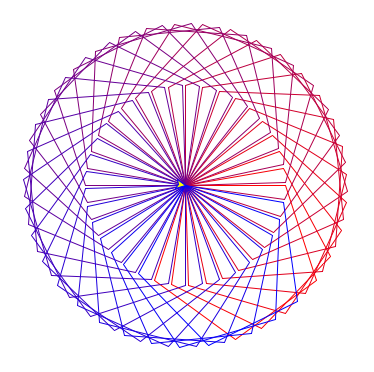

   

   Une rosace colorée créée par juxtaposition de 36 pentagones.

Lors des séances suivantes, nous modifierons des images.